प्रकाशाचा वेग

प्रकाशाचा वेग हा एक वैश्विक स्थिरांक असून त्याला भौतिकशास्त्राच्या अनेक शाखांमध्ये महत्त्व आहे. हा c या आद्याक्षराने दर्शवला जातो व त्याचे अचूक मूल्य २९,९७,९२,४५८ मीटर प्रति सेकंद एवढे आहे. प्रकाशाच्या गतीनुसारच मीटर व सेकंद ही एकके ठरवलेली असल्याने वरील अचूक मूल्य मिळते. विशेष सापेक्षतेनुसार विश्वातील सर्व पदार्थ व माहितीचा सर्वाधिक वेग c आहे तसेच सर्व वस्तुमानहीन कण तसेच सर्व क्षेत्रांमध्ये (उदा. विद्युच्चुंबकीय, गुरुत्वीय, इ.) झालेल्या बदलांच्या प्रसाराचाही हाच वेग असतो. असे कण व लहरी स्रोताच्या गतीचा व निरीक्षकाच्या जडत्वीय संदर्भचौकटीची पर्वा न करता नेहमी c याच वेगाने प्रवास करतात. सापेक्षतावादाच्या सिद्धान्तामध्ये काल-अवकाश परस्परसंबंध दर्शविण्यासाठी तसेच वस्तुमान-ऊर्जा समतुल्यतेच्या E=mc² या प्रसिद्ध सूत्रात cचा आधार घेतला जातो.

पाणी व हवा यांसारख्या पारदर्शक पदार्थांमधून जाताना असलेला प्रकाशाचा वेग हा c पेक्षा कमी असतो. तसेच संदेशतारांमधून जात असतानाही रेडिओ लहरींचा वेग c पेक्षा कमी असतो. या वेगाला जर v मानले तर येणाऱ्या c/v या गुणोत्तरास अपवर्तनांक असे म्हणतात. उदा. काचेचा दृश्यप्रकाशासाठीच्या अपवर्तनांकाचे मूल्य १.५ च्या जवळ आहे. याचा अर्थ प्रकाश हा काचेतून c / १.५ ≈ २,००,००० किलोमीटर प्रतिसेकंद या वेगाने प्रवास करतो. हवेचा अपवर्तनांक १.०००३ आहे म्हणून प्रकाशाची हवेतील गती २,९९,७०० किमी/सेकंद आहे (c पेक्षा ९० किमी/से. ने कमी). मैलांमध्ये प्रकाशाचा वेग सेकंदाला १,८६,२८२ (सुमारे १,८६,०००) मैल आहे.

सामान्यपणे प्रकाश व अन्य विद्युच्चुंबकीय लहरींचे वहन तत्क्षणी होते असे वाटते पण अतिसंवेदनशील उपकरणे व फार मोठी अंतरे असल्यावर त्यांच्या परिमित वेगाचे परिणाम दिसून येतात. दूरवरच्या अवकाशयानांशी संपर्क साधताना संदेशांची देवाणघेवाण करण्यात अनेक मिनिटे किंवा तासही लागू शकतात. ताऱ्यांपासून आपल्याला दिसणारे प्रकाशकिरण त्यांच्यापासून अनेक वर्षांपूर्वी निघालेले असतात. संगणकाची उच्चतम गतीसुद्धा प्रकाशाच्या परिमित गतीमुळे मर्यादित होते कारण संगणकात माहितीचे आदानप्रदान व्हावे लागते. मोठी अंतरे अचूकपणे मोजण्यासाठी प्रकाशाच्या गतीचा उड्डाण-काळ प्रयोगांतून येणाऱ्या माहितीसह वापर करता येतो.

ओलि रोमर याने १६७६ साली गुरूचा उपग्रह आयो याच्या दृश्यगतीचा अभ्यास करून प्रकाशाची गती अनंत नसून ती मर्यादित असल्याचे दाखवून दिले. १८६५ साली जेम्स क्लार्क मॅक्सवेल प्रकाश हा विद्युच्चुंबकीय लहरींचा एक प्रकार असून त्याची गती इतर विद्युच्चुंबकीय लहरींप्रमाणे c इतकी असल्याचे मांडले. अल्बर्ट आइन्स्टाइनने १९०५ साली प्रकाशाची गती c ही कोणत्याही जडत्वीय संदर्भचौकटीच्या सापेक्ष स्थिरच असून प्रकाशस्रोताच्या गतीच्या निरपेक्ष असल्याचे गृहीत धरले. त्याने या गृहीतकाच्या परिणामांचा अभ्यास करून सापेक्षतेचा सिद्धान्त मांडला व असे केल्याने c या स्थिरांचे महत्त्व प्रकाश व विद्युच्चुंबकीय अभ्यासाच्या पलीकडेही असल्याचे दाखवून दिले.

अनेक शतकांच्या परिश्रमाने प्रकाशाच्या वेगाची अधिकाधिक अचूक मूल्ये मिळत गेली. १९७५ साली हे मूल्य २९,९७,९२,४५८ मी/से. आणि अनिश्चितता चार अब्जांश एवढे अचूक मूल्य शोधण्यात आले. १९८३ साली मीटर हे एककच प्रकाशाने निर्वात पोकळीत एका सेकंदात कापलेल्या अंतराचा १/२९९७९२४५८ भाग असे ठरवण्यात आले. त्यामुळे आता cचे सांख्यिक मूल्य मीटर एककानुसार अचूकपणे परिभाषित केले आहे.

निर्वात पोकळीतील प्रकाशाचा वेग सामान्यपणे इंग्रजी "constant" (स्थिरांक) किंवा लॅटिन "celeritas" (चपळपणा) यावरून "c" या आद्याक्षराने दर्शवला जातो.

हेसुद्धा पाहा: विशेष सापेक्षता

निर्वात पोकळीतील प्रकाशाच्या गतीवर प्रकाशस्रोताच्या गतीचा तसेच निरीक्षकाच्या जडत्वीय संदर्भचौकटीचा परिणाम होत नाही. मॅक्स्वेलच्या विद्युच्चुंबकत्वाच्या सिद्धान्ताने प्रभावित होऊन आइन्स्टाईनने प्रकाशाच्या गतीचे स्थिर मूल्य १९०५ साली मांडले. त्याच्या गृहीतकाला नंतरच्या प्रयोगांमधून पुष्टी मिळालेली आहे. प्रकाशाची केवळ द्विमार्ग गती (स्रोताकडून आरशाकडे व परावर्तित होऊन पुन्हा स्रोताकडे) जडत्वचौकटीपासून मुक्त असल्याचे सिद्ध करता येते, कारण प्रकाशाची एकमार्गी गतीचा (स्रोताकडून दूरवरच्या शोधकाकडे) वेग ठरवणे हे अशक्य आहे. परंतु घडाळ्यांसाठी आइन्स्टाईन समक्रमितेचा स्वीकार केल्यास एकमार्गी व द्विमार्गी गती संज्ञेनुसार समान होतात. जडत्वीय संदर्भचौकटींमध्ये भौतिकशास्त्राचे नियम समान आहेत हे मानून cच्या अचलत्वाच्या परिणामांचा अभ्यास सापेक्षतेच्या विशेष सिद्धान्तामध्ये होतो. याचा एक परिणाम म्हणजे प्रकाशासह सर्व वस्तुमानहीन कण व लहरी निर्वात पोकळीत c याच वेगाने प्रवास करू शकतात.

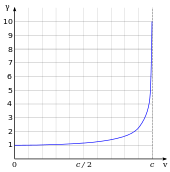
विशेष सापेक्षतेचे अविश्वसनीय व प्रायोगिकरीत्या सिद्ध झालेले अनेक परिणाम आहेत. यांमध्ये वस्तुमान-ऊर्जा समतुल्यता, लांबीचे आकुंचन (गतिमान वस्तूंची लांबी घटते) व वेळ कमी होणे (गतिमान घड्याळे कमी वेळ दाखवतात) यांचा समावेश होतो. कालगती मंदावणे व लांबीचे आकुंचन हे दोन्ही परिणाम γ या गुणकाच्या पटीत असतात. या गुणकास लॉरेन्ट्झ गुणक असे संबोधले जाते व त्याचे मूल्य γ = (1 − v²/c²)^−1/2 या सूत्राद्वारे काढता येते, जिथे v हा त्या वस्तूची गती दर्शवतो. सामान्य जीवनात γ व १ यांतील फरक अगदीच किरकोळ असतो. अशावेळी गॅलिलिअन सापेक्षतेचा वापर करता येतो. परंतु सापेक्षकीय गती असता γचे मूल्य वाढू लागते व जेव्हा vची किंमत cच्या जवळ जाते तेव्हा γ अनंताकडे जाऊ लागतो.

विशेष सापेक्षतेच्या सिद्धान्ताचा सारांश हा अवकाश व काळ यांना काल-अवकाश अशी एक एकसंध रचना मानून भौतिकीय सिद्धान्तांना लॉरेन्ट्झ अचलता या विशेष सममितीची अट पूर्ण करण्यास भाग पाडणे असा सांगता येतो. लॉरेन्ट्झ अचलता हे पुंज विद्युत्गतिकी, पुंज कालगतिकी, कणभौतिकीची प्रमाण प्रतिकृती व साधारण सापेक्षता अशा आधुनिक भौतिकशास्त्रीय सिद्धान्तांसाठीचे एक जवळपास वैश्विक गृहीतक आहे. त्यामुळे c हा स्थिरांक आधुनिक भौतिकशास्त्रात सर्वव्यापी आहे व तो प्रकाशाशी काही संबंध नसलेल्या क्षेत्रांतही आढळतो. उदाहरणार्थ गुरुत्वाकर्षणाचा व गुरुत्वीय लहरींचा वेग हा c असल्याचे साधारण सापेक्षता वर्तवते.

सामान्यपणे असे गृहीत धरले जाते की प्रकाशाची गती व अन्य वैश्विक स्थिरांक मूल्य सर्व काल-अवकाशात समानच असतात, म्हणजे स्थानानुसार किंवा वेळेनुसार त्यांच्या मूल्यांत काहीही बदल होत नाही. परंतु अनेक नवीन सिद्धांतांमध्ये प्रकाशाचा वेग काळानुसार बदलला असल्याचे मांडले गेले आहे. याबाबत अजूनपर्यंत काहीही निर्णायक पुरावे निरीक्षणातून आढळले नाहीत, पण हा चालू संशोधनाचा महत्त्वाचा विषय उरला आहे.

विशेष सापेक्षतेनुसार m हे स्थिर वस्तुमान व v वेग असलेल्या वस्तूची ऊर्जा ही γmc² इतकी असते, जिथे γ हा लॉरेन्ट्झ गुणक आहे. वेग शून्य असल्यास γ एक होतो व यावरूनच E = mc² हे वस्तुमान-ऊर्जा समतुल्यतेचे प्रसिद्ध सूत्र तयार होते. जेव्हा v व c समान होऊ लागतात तेव्हा लॉरेन्ट्झ गुणकाचे मूल्य अनंतापर्यंत जाते. याचा अर्थ असा की वस्तुमान असलेल्या वस्तूला प्रकाशगतीपर्यंत त्वरण देण्यास अनंत ऊर्जा लागेल. स्थिर वस्तुमान धन असलेल्या सर्व वस्तूंच्या वेगाची उच्चतम मर्यादा ही प्रकाशाची गती असून फोटॉनसुद्धा त्यापेक्षा वेगाने जाऊ शकत नाहीत, हे अनेक प्रयोगांतून सिद्ध झालेले आहे.

सामान्य भौतिकशास्त्रात प्रकाशाला विद्युच्चुंबकीय लहर मानण्यात आले आहे. विद्युच्चुंबकीय क्षेत्राचे गुणधर्म हे मॅक्स्वेलच्या समीकरणांनुसार सांगता येतात, ज्यानुसार निर्वात पोकळीतील विद्युच्चुंबकीय लहरींचा वेग c व विद्युत् स्थिरांक ε₀ व चुंबकीय स्थिरांक μ₀ यांच्यामध्ये संबंध प्रस्थापित होतो:

${\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ .}$

पारदर्शक व अर्धपारदर्शक माध्यमांतून जाताना प्रकाशाची गती c पेक्षा कमी असते. तसेच भिन्न प्रकारच्या (रंगाच्या) लहरींचा वेगही भिन्न असतो.

इसवी सनापूर्वी किमान पाच ते सहा हजार वर्षांपूर्वी लिहिल्या गेलेल्या ऋग्वेदाच्या पहिल्या मंडलात, पन्नासाव्या सूक्तातील, चौथ्या श्लोकात म्हणले आहे की
तरणिर्विश्वदर्शतो ज्योतिष्कृदसि सूर्य ।
विश्वमा भासि रोचनम् ॥ ऋग्वेद १.५०.४

अर्थ :- हे सूर्या, गतीने भारलेला तू, सर्वांना दिसतोस. तू प्रकाशाचा स्रोत आहेस. तू साऱ्या जगाला प्रकाशमान करतोस.

पुढे चौदाव्या शतकात, विजयनगर साम्राज्यातील सायणाचार्य (१३३५ – १३८७) ह्या शास्त्रज्ञाने ऋग्वेदाच्या ह्या श्लोकाची मीमांसा करताना लिहिले –

तथाच स्मर्यते योजनानां सहस्त्रं द्वे द्वे शते द्वे च
योजने एकेन निमिषार्धेन क्रममाण नमोऽस्तुते॥ – सायण ऋग्वेद भाष्य १.५०.४

अर्थ :-
प्रकाशाने पार पडलेले अंतर २,२०२ योजने (द्वे द्वे शते द्वे..)
१ योजन = ९ मैल, ११० यार्ड्‌स = ९.०६२५ मैल (कशावरून?)
अर्थात प्रकाशाचे अंतर ९.०६२५ X २२०२ = २१,१४४.७०५ मैल
घेतलेला वेळ अर्धा निमिष = १/८.७५ सेकंद = ०.११४२८ सेकंद (कशावरून?)
अर्थात प्रकाशाचा वेग १८५,०२५.८१३ मैल / सेकंद
आधुनिक गणनेनुसार प्रकाशाचा वेग सेकंदाला १,८६,२८२.३९७ मैल.